ggaaooppeenngg

为什么计算机科学是无限的但生命是有限的

LC-trie 快速路由查找算法

发表于 更新于 Disqus：

一般来说我们把字典树称作 trie，这是一个用于查找字符串的数据结构，举个简单的例子。下面就是一个把 b，abc，abd，bcd，abcd，efg，hii 这 6 个单词构造成字典树的例子。

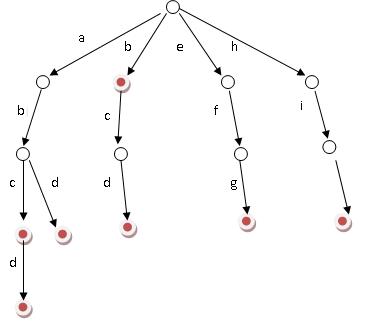
在路由表中我们可以把子网看作一个二进制字符串，对于 IPv4 来说，字符串的长度就有 32 位。

以上面这个为例子，有编号 0 到 14 这几个二进制的字符串（字符集和只有 0 和 1），右边是他们的具体字符串，这样的字典树有一点像二叉树。如果把它画出来是这样的。

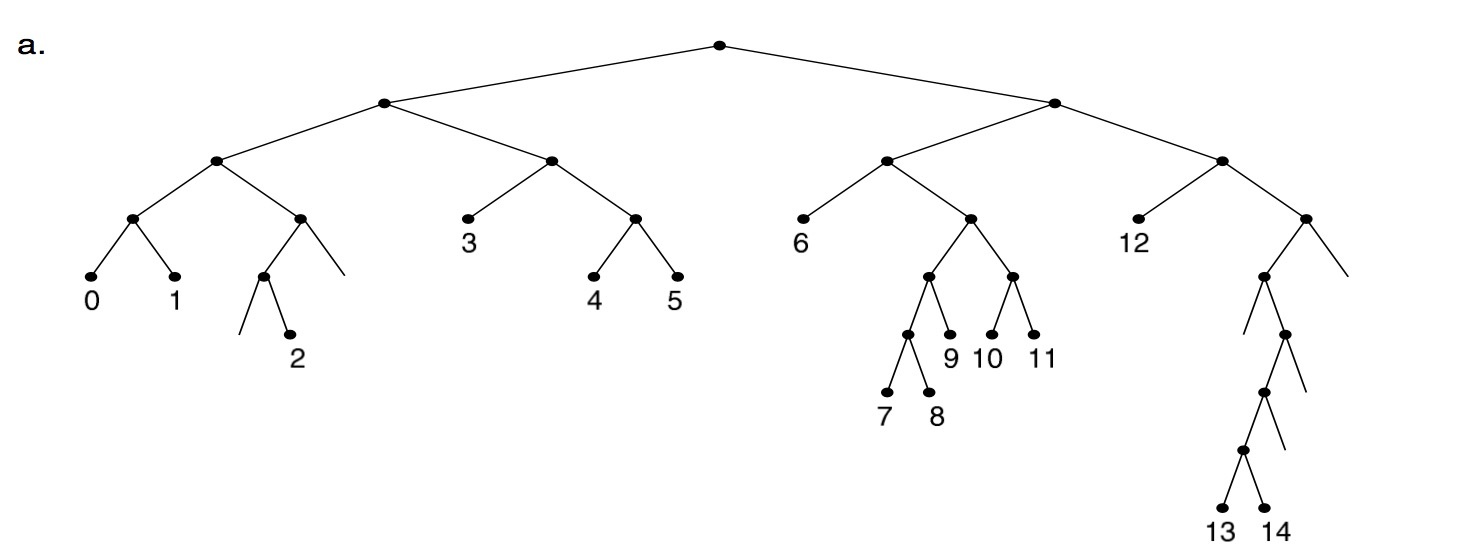
对这个树做压缩有一个办法就是把单节点作压缩，形成下面这个树，这个就是路径压缩，path compressed trie。

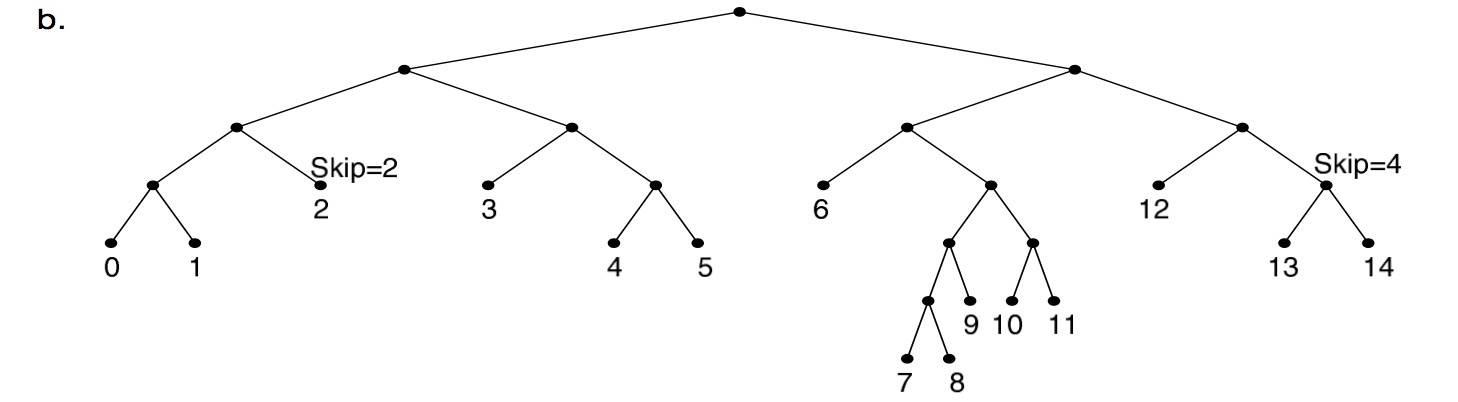
我们需要在压缩的地方进行标记，比如 skip 4 那里把一段 1011 压缩掉了。而 LC-trie 指的是 Level Compressed trie，这个树会把层级进行压缩，因为我们得到的这个字典树实际上是一个稀疏树，高度并不是平衡的，所以为了达到平衡，需要做的一件事情是把高度进行压缩，压缩之后变成下面这个形式，这样整棵树就会更加扁平。

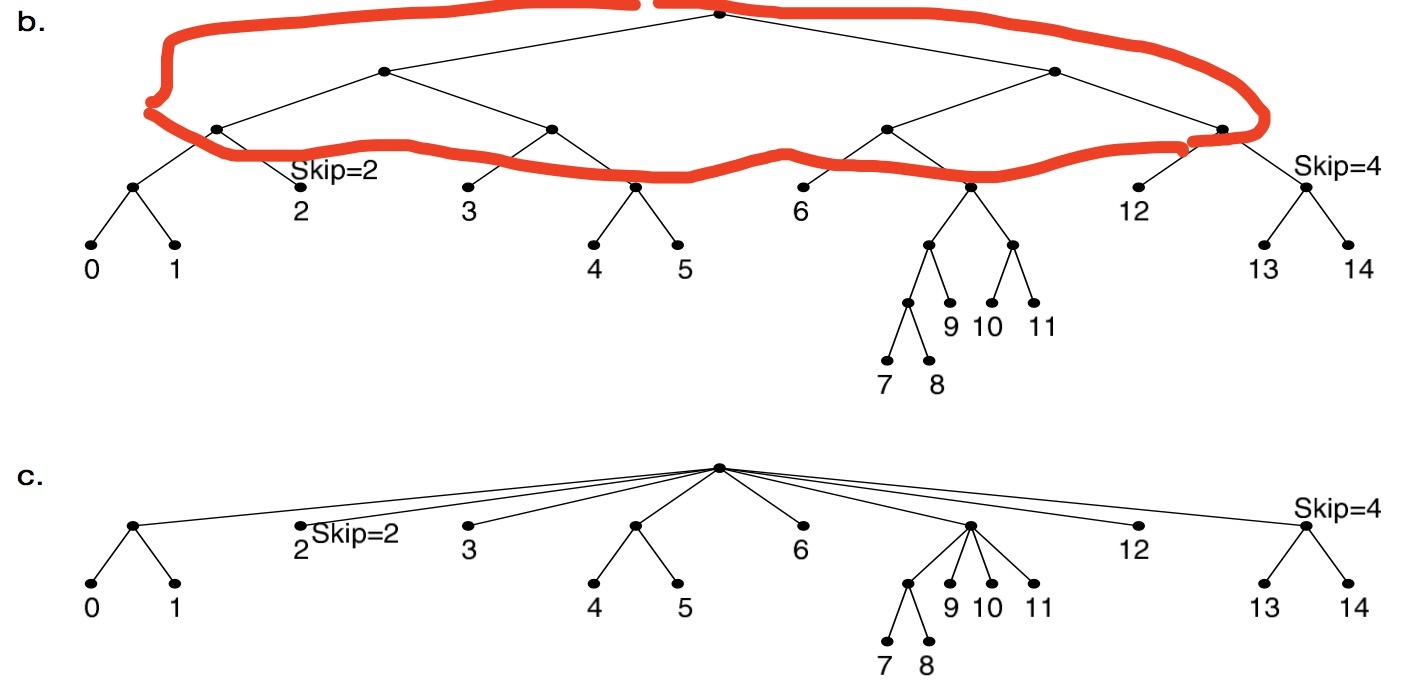
这个树是有两种类型的节点，一种是 leaf，保存了路由具体的信息的叶子结点，一种是 trie node（tnode）保存了中间节点，子节点可能是 tnode 或者 leaf。trie 上有几个数据要存储，一个是 bits，这个表示的是子节点的选择度（这个怎么理解呢，就是我接下来的子节点是八叉了，因为我把原来的树压缩了，所以现在不需要二选一，现在直接来个八选一就可以），对于一个八叉的压缩来说，就要有一个 3 位的数字来存储，也就是 log(8)，当然也可以能是 7 叉，但是必须是 2 的指数。而 pos 表示的是从那个 bit 开始，它的作用和 skip 类似只不过不是一个相对值，而是一个累加值，表示我们要从哪开始（从字符串的起始位置开始数）。

我们先看一下搜索的代码，其实很简单，就是不断匹配公共前缀直到直到找到叶子节点（ bits == 0）。匹配前缀的方式比较 tricky，用异或进行确认。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/* rcu_read_lock needs to be hold by caller from readside */
static struct key_vector *fib_find_node(struct trie *t,
					struct key_vector **tp, u32 key)
{
	struct key_vector *pn, *n = t->kv;
	unsigned long index = 0;

	do {
		pn = n;
		n = get_child_rcu(n, index);

		if (!n)
			break;

		index = get_cindex(key, n);

		/* This bit of code is a bit tricky but it combines multiple
		 * checks into a single check.  The prefix consists of the
		 * prefix plus zeros for the bits in the cindex. The index
		 * is the difference between the key and this value.  From
		 * this we can actually derive several pieces of data.
		 *   if (index >= (1ul << bits))
		 *     we have a mismatch in skip bits and failed
		 *   else
		 *     we know the value is cindex
		 *
		 * This check is safe even if bits == KEYLENGTH due to the
		 * fact that we can only allocate a node with 32 bits if a
		 * long is greater than 32 bits.
		 */
		if (index >= (1ul << n->bits)) {
			n = NULL;
			break;
		}

		/* keep searching until we find a perfect match leaf or NULL */
	} while (IS_TNODE(n));

	*tp = pn;

	return n;
}

具体看一下 get_cindex 匹配的方式，#define get_cindex(key, kv) (((key) ^ (kv)->key) >> (kv)->pos)，对 tnode 和 被比较的 key 做异或，这个怎么理解呢，看下面的图的例子这是正确匹配以后的结果，灰色代表 0，蓝色代表 1，两个值进行异或的话，首先 pos 会被右移掉，然后 bits 的部分会原样保留，因为 tnode 的这部分都是 0。然后亲址的部分如果完全匹配的话结果就都是 0 ，但是如果不完全匹配的话，结果就会比 index 还要大，因为高位还有 1，所以这就是为什么 index >= (1ul << n->bits 能判断是否匹配的前缀的原因。

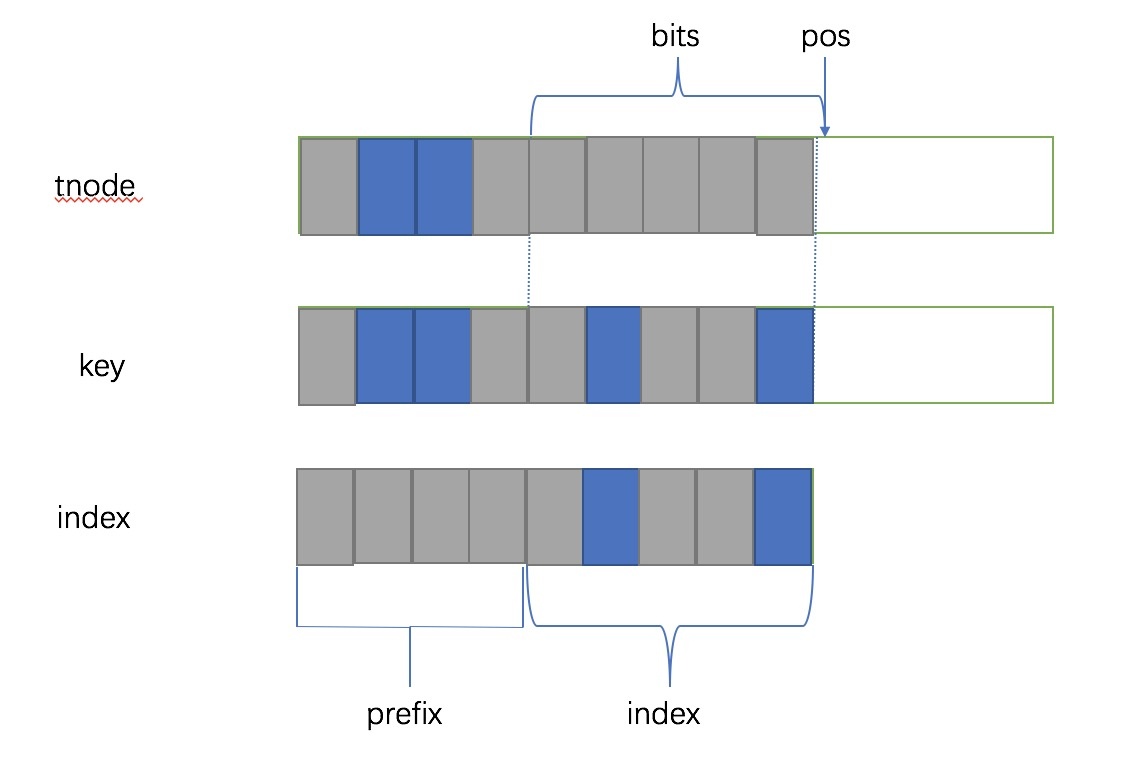
然后我们再看一下插入的流程。首先算出匹配到当前节点的子节点（有可能有，有可能没有）。

1
2
3
4
5
6
7
8
9
10
11
12

static int fib_insert_node(struct trie *t, struct key_vector *tp,
			   struct fib_alias *new, t_key key)
{
	struct key_vector *n, *l;

	l = leaf_new(key, new);
	if (!l)
		goto noleaf;

	/* retrieve child from parent node */
	n = get_child(tp, get_index(key, tp));

如果有子节点，就要创建一个新的 tnode，再把这个 key 给插入。

1
2
3
4
5
6
7
8
/* Case 2: n is a LEAF or a TNODE and the key doesn't match.
 *
 *  Add a new tnode here
 *  first tnode need some special handling
 *  leaves us in position for handling as case 3
 */
if (n) {
	struct key_vector *tn;

__fls find last set bit，就是找到 pos，然后扩展出有两个选择（2 的 1 次方）的 tnode。

1
2
3
tn = tnode_new(key, __fls(key ^ n->key), 1);
if (!tn)
	goto notnode;

设置 tn 的 父节点为 tp，然后把 key 插入到 tn 当中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
	/* initialize routes out of node */
	NODE_INIT_PARENT(tn, tp);
	put_child(tn, get_index(key, tn) ^ 1, n);

	/* start adding routes into the node */
	put_child_root(tp, key, tn);
	node_set_parent(n, tn);

	/* parent now has a NULL spot where the leaf can go */
	tp = tn;
}

/* Case 3: n is NULL, and will just insert a new leaf */
node_push_suffix(tp, new->fa_slen);
NODE_INIT_PARENT(l, tp);
put_child_root(tp, key, l);

开始进行平衡调整树形。

1
2
3
4
5
6
7
8
	trie_rebalance(t, tp);

	return 0;
notnode:
	node_free(l);
noleaf:
	return -ENOMEM;
}

再看一下树的高度是如何进行调整的，从当前节点一直向上压缩。

1
2
3
4
5
static void trie_rebalance(struct trie *t, struct key_vector *tn)
{
	while (!IS_TRIE(tn))
		tn = resize(t, tn);
}
1
2
3
4
5
6
#define MAX_WORK 10
static struct key_vector *resize(struct trie *t, struct key_vector *tn)
{
#ifdef CONFIG_IP_FIB_TRIE_STATS
	struct trie_use_stats __percpu *stats = t->stats;
#endif

利用 container_of 获取父节点。

1
struct key_vector *tp = node_parent(tn);

获取子节点，初始化 max_work 为 10。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
unsigned long cindex = get_index(tn->key, tp);
int max_work = MAX_WORK;

pr_debug("In tnode_resize %p inflate_threshold=%d threshold=%d\n",
	 tn, inflate_threshold, halve_threshold);

/* track the tnode via the pointer from the parent instead of
 * doing it ourselves.  This way we can let RCU fully do its
 * thing without us interfering
 */
BUG_ON(tn != get_child(tp, cindex));

/* Double as long as the resulting node has a number of
 * nonempty nodes that are above the threshold.
 */

should_inflate 决定要不要压缩的依据是根据动态压缩算法来的（引用4），直观的来说就是高度超过了一个动态计算的阈值，并且还没压缩超过十次就会继续压缩。这个动态阈值的算法是用非空子节点的数目如果超过压缩之后子节点数目的一半就值得压缩。而 inflate 做的事情就把层级压缩一层，也就是把 children 的 children 按照 bits 的匹配放到 parent 的 new_children 当中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
	while (should_inflate(tp, tn) && max_work) {
		tp = inflate(t, tn);
		if (!tp) {
#ifdef CONFIG_IP_FIB_TRIE_STATS
			this_cpu_inc(stats->resize_node_skipped);
#endif
			break;
		}

		max_work--;
		tn = get_child(tp, cindex);
	}

	/* update parent in case inflate failed */
	tp = node_parent(tn);

	/* Return if at least one inflate is run */
	if (max_work != MAX_WORK)
		return tp;

到这里说明一次调整都没有发生，说明节点很稀疏，也就是把节点分开。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
	/* Halve as long as the number of empty children in this
	 * node is above threshold.
	 */
	while (should_halve(tp, tn) && max_work) {
		tp = halve(t, tn);
		if (!tp) {
#ifdef CONFIG_IP_FIB_TRIE_STATS
			this_cpu_inc(stats->resize_node_skipped);
#endif
			break;
		}

		max_work--;
		tn = get_child(tp, cindex);
	}

只有一个孩子，可以进行 path compress，没必要再多一个中间节点。

1
2
3
4
5
6
7
	/* Only one child remains */
	if (should_collapse(tn))
		return collapse(t, tn);

	/* update parent in case halve failed */
	return node_parent(tn);
}

整个的 LC-trie 的结构大致如此，主要用于路由表中路由规则的快速匹配，是在 3.6 之后引进的，摒弃了之前用哈希来查找路由表的算法。

引用

  1. The-Art-Of-Programming-By-July
  2. Fast address lookup for Internet routers
  3. LC-trie implementation notes
  4. Implementing a dynamic compressed trie