贝叶斯优化之高斯过程和应用
贝叶斯优化(BO)
贝叶斯优化是一种黑盒优化方法,一般有几个特征:
输入纬度不大,一般小于 20 个,时间复杂度是$O(n^3)$
有设定的取值空间
目标函数需要是连续的(我觉得这个好像不是必须的,离散的也可以)
目标函数的计算非常消耗成本(时间等等)
目标函数是黑盒的,没有明确的结构
目标函数(derivative-free)没有一阶二阶导数(不然就可以用梯度下降去算了)
因为这些特性,在做机器学习的超参数调优的时候特别合适。
BayesOpt consists of two main components: a Bayesian statistical model for modeling the objective function, and an acquisition function for deciding where to sample next.
贝叶斯优化主要是要两个部分,一个是统计模型比如高斯过程(GP),一个是采样函数(AC)决定下一个样本从拿里获取。
高斯过程(GP)
高斯过程是贝叶斯优化中的一种统计模型,先抛开具体的数学问题,简单讲一下就是,假设我在一个变量空间(比如多个超参数)采样了一个目标函数(我们训练结果的 evaluation),然后我们会得到一个后验分布,这就类似条件概率里面,我们知道了某个事情发生以后,如果随机变量是相关的,我们有更大的概率确定其他变量的分布。例如下图,绿色是我们的分布空间,每次采样以后,分布的空间就会缩小,进而接近我们的曲线。
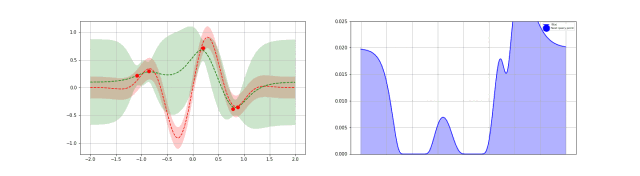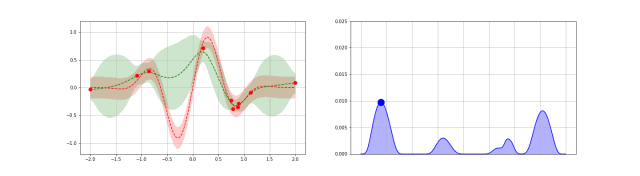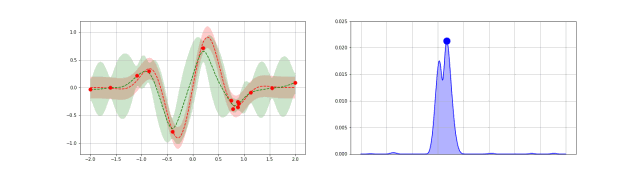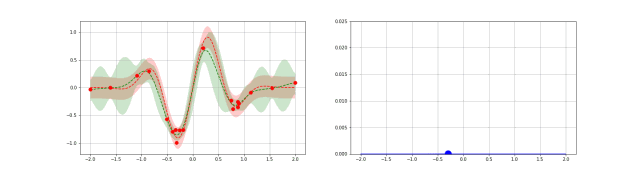
从数学上描述这件事情就需要高斯分布和高斯过程了。高斯分布我相信大家都耳熟能详,他由平均值 $\mu$ 还有标准差 $\sigma$ 决定分布。高斯过程的本质是一个多元高斯分布,只不过他是无限空间上的,定义高斯过程需要一个核函数定义他的协方差矩阵,也就是一个矩阵定义多个随机变量的相关性。当然了,有限的离散点用协方差矩阵可以,如果取值是连续的就需要核函数描述这个“无限”的协方差矩阵了。
协方差的核函数就很多选项,A Visual Exploration of Gaussian Processes 提供了一个非常 intuitive 的可视化来解释 GP 和各种描述协方差矩阵的核函数。
高斯过程被定义为一个随机过程,相当于每个样本点自己也是个随机函数,对于高斯分布来说,每个样本点也是一个高斯分布函数就是高斯过程,cs4780 的 Lecture 15有非常详细的解释。
Definition: A GP is a (potentially infinte) collection of random variables (RV) such that the joint distribution of every finite subset of RVs is multivariate Gaussian:
$ f \sim GP(\mu, k), $
where $\mu(\mathbf{x})$ and $k(\mathbf{x}, \mathbf{x}’)$ are the mean resp. covariance function! Now, in order to model the predictive distribution $P(f_* \mid \mathbf{x}_*, D)$ we can use a Bayesian approach by using a GP prior: $P(f\mid \mathbf{x}) \sim \mathcal{N}(\mu, \Sigma)$ and condition it on the training data $D$ to model the joint distribution of $f=f(X)$ (vector of training observations) and $f_* = f(\mathbf{x}_*)$ (prediction at test input).
采样函数
采样函数一般有 expected improvement(EI),当然还有 probability improvement(PI), upper confidence bound(UCB), knowledge gradient(KG),entropy search and predictive entropy search 等等。
采样的策略有两种:
Explore:探索新的点,这种采样有助于估计更准确的;
Exploit:利用已有结果附近的点进行采样,从而希望找到更大的;
这两个标准是互相矛盾的,如何在这两者之间寻找一个平衡点可以说是采样函数面对的主要挑战。
Expected improvement is a popular acquisition function owing to its good practical performance and an analytic form that is easy to compute. As the name suggests it rewards evaluation of the objective $f$ based on the expected improvement relative to the current best. If $f^* = \max_i y_i$ is the current best observed outcome and our goal is to maximize $f$, then EI is defined as
$\text{EI}(x) = \mathbb{E}\bigl[\max((f(x) - f^*), 0)\bigr]$
在 Facebook 的 Ax 在这里提到使用了 PyTorch 的一个 BoTorch 用的就是 EI,就是期望的增加度。
高斯分布式的期望就是 $\mu$ 所以是很好算的,$f^*$ 是已知的定值,这里有一个计算的推导。
BoTorch 提供了一个优化的 EI 叫 Noisy EI,主要功能是抗噪。
The above definition of the EI function assumes that the objective function is observed free of noise. In many types of experiments, such as those found in A/B testing and reinforcement learning, the observations are typically noisy. For these cases, BoTorch implements an efficient variant of EI, called Noisy EI, which allow for optimization of highly noisy outcomes, along with any number of constraints (i.e., ensuring that auxiliary outcomes do not increase or decrease too much). For more on Noisy EI, see our blog post.
这是采样的过程的一个示例:
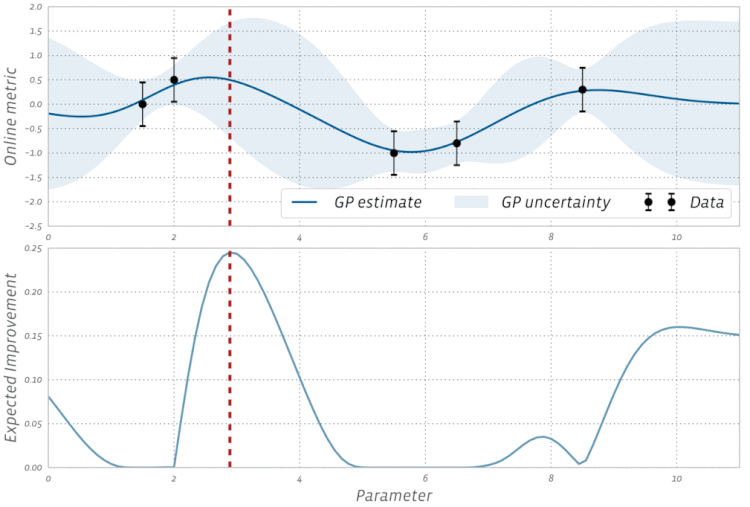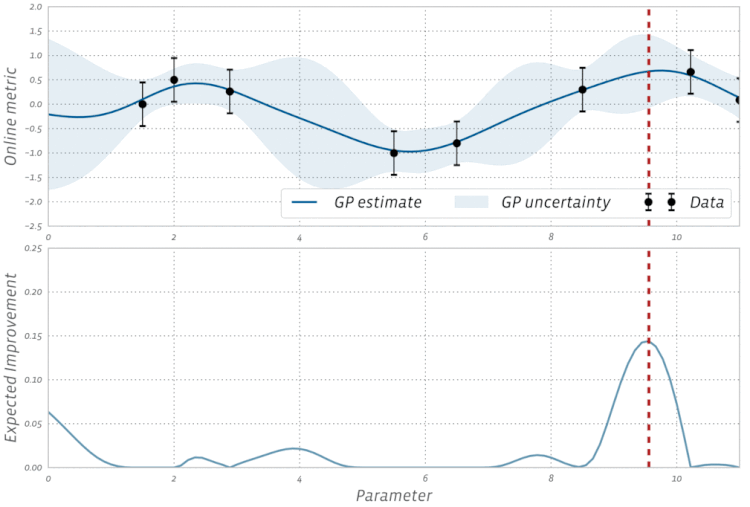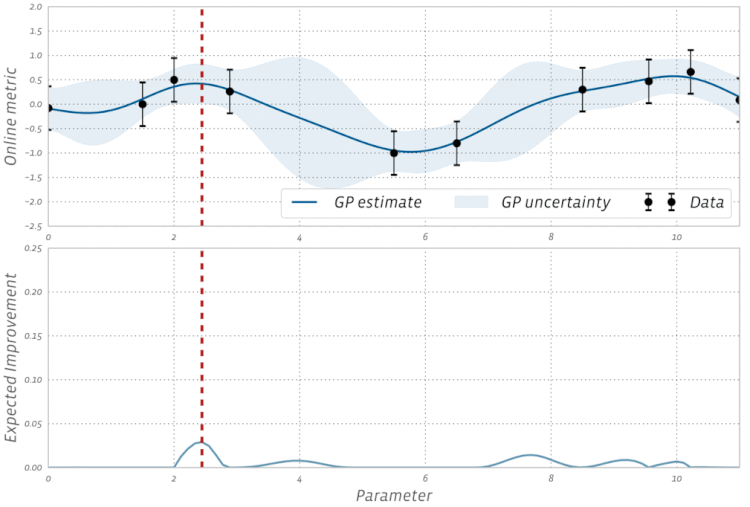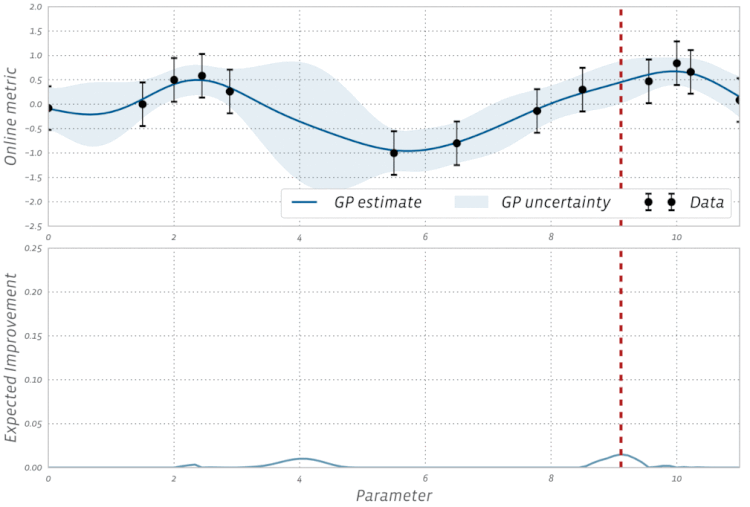
应用
高斯过程本身可以用来回归和分类,使用高斯过程的贝叶斯优化有很多具体的应用场景,除了超参数优化之外,对于网络结果(层数,数据并行度)等等也是可以使用的。
除此之外像 horovod 也使用了贝叶斯优化,在这个目录下面。
Horovod comes with several adjustable “knobs” that can affect runtime performance, including –fusion-threshold-mb and –cycle-time-ms (tensor fusion), –cache-capacity (response cache), and hierarchical collective algorithms –hierarchical-allreduce and –hierarchical-allgather.
他主要是服务于一些 Tensor Fusion 和 response cache 等参数以及层级 collective 通信选择,文档提到了通过设置一些参数细致控制调优的过程。